What are loops?
In Kumu, the three basic items you can create are elements, connections, and loops.
Visually speaking, elements are circles, connections are lines between the elements, and loops are groups of two or more connections.
Loops show up on the map as a text label, and the default position of that label is in the middle of all the connections that are part of the group.
You can use these visual tools in all kinds of different ways, but here are some common uses that we see:
| Elements | Connections | Loops |
|---|---|---|
| Factors in a system (causes and effects) | Cause-and-effect relationships | Causal loops |
| Stocks | Flows | Sub-systems |
| Decisions, chances, and ends in a decision tree | Paths along the decision tree | Multi-part decisions |
| Steps in a process | Paths from one step to the next | Sub-processes |
| People | Interpersonal relationships | Sub-networks or communities |
| People & organizations | Connect people to the organizations they're affiliated with | Sub-networks or communities |
| Authors & books/articles they've co-authored | Connect authors to their books/articles | Sub-networks or communities |
| Stakeholders & areas of interest | Connect stakeholders to the areas they're interested in | Sub-networks or communities |
| Funders, non-profits, and population groups | Connect funders to non-proftis, and connect non-profits to the populations they serve | Sub-networks or communities |
| Companies and sectors/industries | Connect companies to their sectors/industries | Sub-networks or communities |
Creating a loop
To create a loop, you can click the green button at the bottom of your map and select "Add loop". Then, click on the connections you want to include in the loop, then add a descriptive loop label below and press enter on your keyboard.
If you want to edit a loop, click on the loop's label to open its profile in the left side panel. In the bottom right corner of the profile, click the pencil icon to select and de-select connections that are a part of the loop.
Click & drag the loop label to move it, or hold down Option on your keyboard (Alt on Windows) and click & drag to move the entire loop, including all its elements and connections, while maintaining their structure.
Identifying loops in systems
Colloquially, you can use the word “loop” to describe any kind of line that curves around in a circle or an oval. When you’re mapping systems in Kumu, you’ll find many groups of connections that meet that definition, but they aren’t necessarily the loops that a system mapper is looking for.
In a system map, a great litmus test for discovering loops is to ask the question, “If I follow the arrows in this group of connections, can I get trapped?” If the answer is yes, you’ve found a loop!
If not, the structure is not a loop, but might still be complex enough to deserve some further study.
Here’s an example of a structure that looks like a loop, but is not, because no matter which arrow you follow, you always end up at the same factor, escaping the trap:
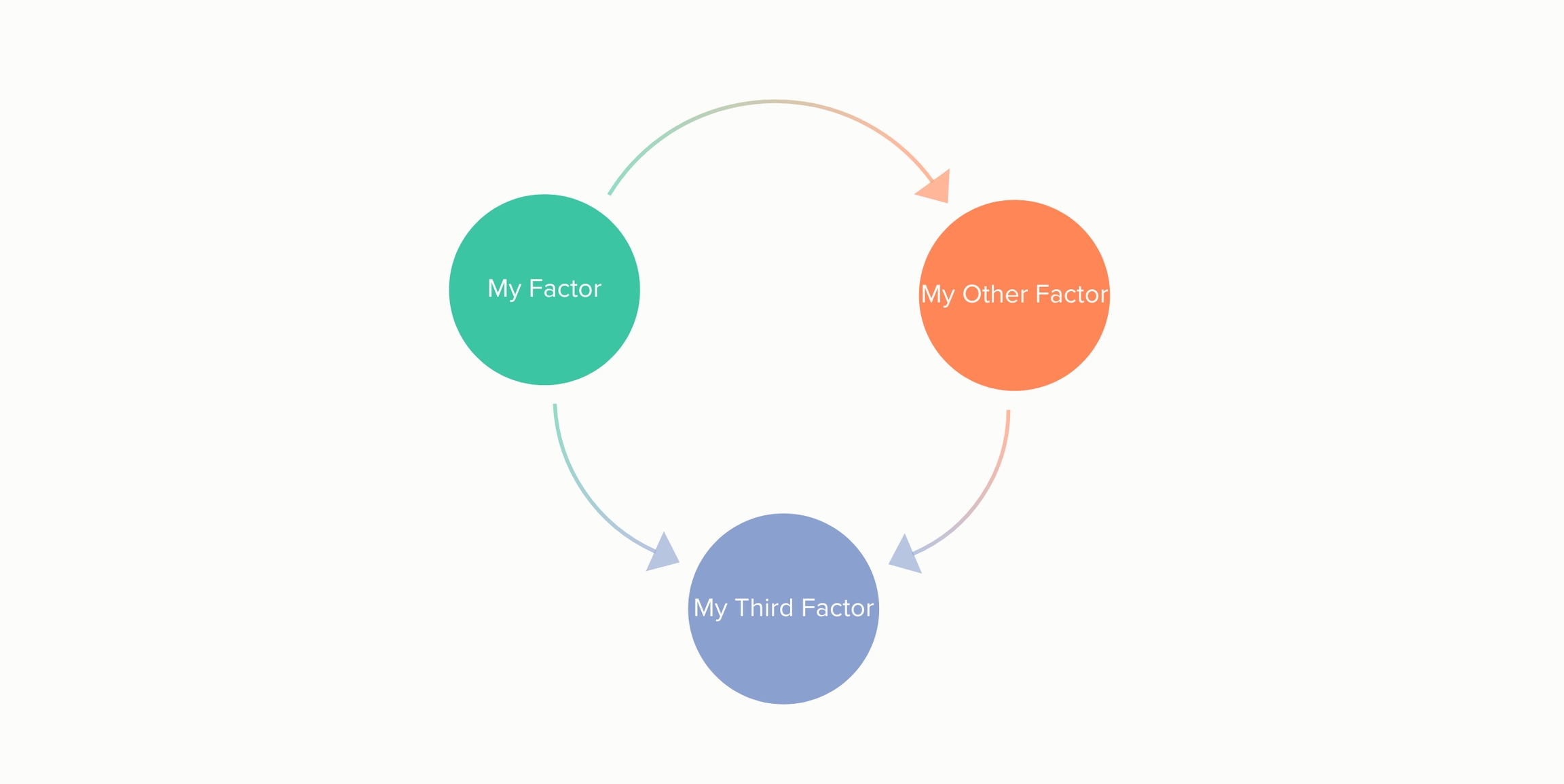
On the other hand, if you reverse just one of the arrows in the structure, you inevitably get trapped going around and around in a circle:
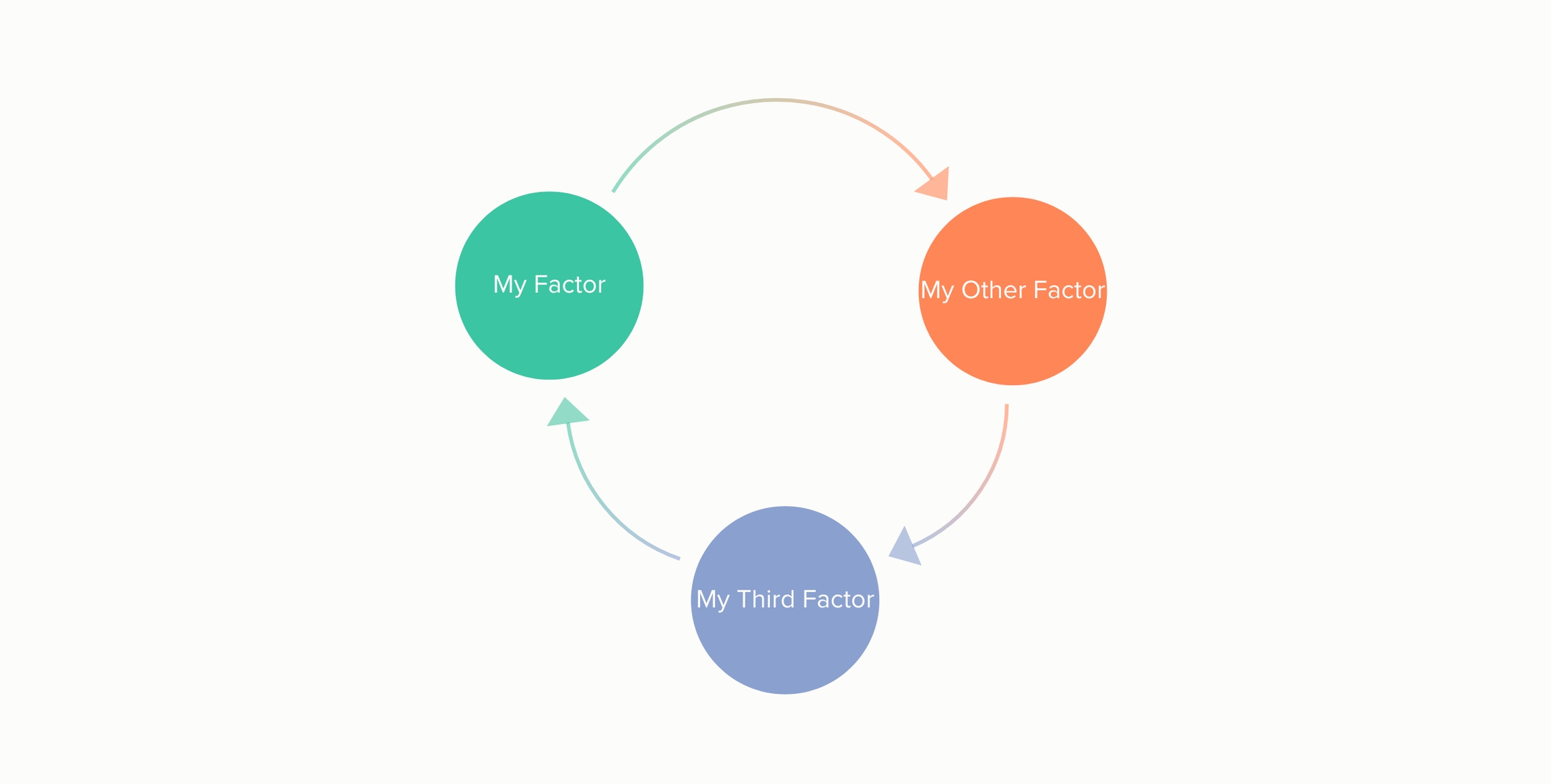
This is the kind of loop you’re looking for in a system map.
It’s rarely so simple—in many cases, your loops will contain more than three connections, and they likely won’t be laid out in such a nice, circular shape. You'll also have the rest of the elements and connections in the map contending for your attention. This is where loop detection comes in handy!
Loop detection
We finally added the much-awaited feature that allows you to detect loops automatically!
To detect loops, follow these steps:
- Create your map with some elements and connections, as you would normally.
- Click on the green plus icon at the bottom of your map, and choose "Add loop".
- Click "detect loops automatically".
- A menu will pop up on the left side of your map with the detected loops.
Some things to note:
- Loops are ranked from shortest (least amount of elements) to longest (most elements).
- You can hover over any loop name to showcase it on the map and see which elements/connections are a part of it.
- Click on any loop number to give it a name and save it. Unnamed loops are not saved in your dataset!
- Adding a name to a loop will add that label to your map in the center of the loop.
- Loops can only be exported with JSON. You can't export loops to Excel.
Automatic loop detection is not (yet) available for maps imported with Google Sheets. If you'd like to use loop detection, please import your map with Excel.
Decorating loops
Once you've identified your loops, you might want to customize how they look! One common thing to change is your loops' font size. This can be done in the Advanced Editor, like so:
loop {
font-size: 40; // Replace with any number
}
This code will change the font size for all loops. If you just want to change the size for a specific loop, you can use a selector. Here's an example that selects by label to decorate one loop:
// replace My Specific Loop with the label of your loop
loop[Label = "My Specific Loop"] {
font-size: 40;
}
Less common, but still useful, is to categorize loops with types like Vicious, Virtuous, Stagnating, and Stabilizing, then color-code by those loop types. If you add those types to the Loop Type field (under the Label in the profile), you can use this code to color code automatically:
loop {
font-color: categorize("Loop Type", olympic)
}
You can replace olympic with the name of any of our color palettes.
results matching ""
